请耐心看完这篇博文。每一个人学习机器学习几乎都是从用MNIST数据集来做手写数字图像识别开始的，但是我希望这个教程和其他的有所不同。

我记得当TensorFlow在2015年11月被发布的时候，我按照这个《为TensorFlow初学者准备的MNIST教程》里面的步骤，盲目地复制和粘贴其中所有的代码到我的命令行终端。然后一些数字按照它们本应该出现的样子跳了出来。我想“OK，我知道有些神奇的事情发生了。但为什么我看不到它们?”所以我写这篇博文的目的就是制作一个既有交互性还能有可视化的MNIST教程。同时还希望能教给你一两件其他的教程仅仅假定你知道的事情。

这个教程里，我会使用TensorFlow的机器学习库，并基于Ubuntu 14.04版和Python3。如果你想了解如何在你自己的系统里安装TensorFlow，可以在这里查看我的其他教程。

如果你还没有安装numpy和matplotlib库，你需要安装他们。请打开一个Ubuntu命令行终端，并敲入如下的一行命令：

$ sudo apt-get install python-numpy python3-numpy python-matplotlib python3-matplotlib

首先，我们需要在终端里开启一个python命令行编辑器，并用如下几行代码导入MNIST数据集（和其他python的依赖库）：

from tensorflow.examples.tutorials.mnist import input_data

mnist = input_data.read_data_sets(‘MNIST_data’, one_hot=True)

import matplotlib.pyplot as plt

import numpy as np

import random as ran

接着让我们定义几个函数，用来指定从数据集里导入的训练和测试数据的数量。这些代码并不是特别紧要，除非你希望能了解它们背后的逻辑。

你需要复制粘贴每个函数，并在终端里敲两次回车。

def TRAIN_SIZE(num):

print (‘Total Training Images in Dataset = ‘ + str(mnist.train.images.shape))

print (‘————————————————–‘)

x_train = mnist.train.images[:num,:]

print (‘x_train Examples Loaded = ‘ + str(x_train.shape))

y_train = mnist.train.labels[:num,:]

print (‘y_train Examples Loaded = ‘ + str(y_train.shape))

print(”)

return x_train, y_train

def TEST_SIZE(num):

print (‘Total Test Examples in Dataset = ‘ + str(mnist.test.images.shape))

print (‘————————————————–‘)

x_test = mnist.test.images[:num,:]

print (‘x_test Examples Loaded = ‘ + str(x_test.shape))

y_test = mnist.test.labels[:num,:]

print (‘y_test Examples Loaded = ‘ + str(y_test.shape))

return x_test, y_test

我们还要定义两个简单的函数来重新排列图像尺寸并显示这些图像数据：

def display_digit(num):

print(y_train[num])

label = y_train[num].argmax(axis=0)

image = x_train[num].reshape([28,28])

plt.title(‘Example: %d  Label: %d’ % (num, label))

plt.imshow(image, cmap=plt.get_cmap(‘gray_r’))

plt.show()

def display_mult_flat(start, stop):

images = x_train[start].reshape([1,784])

for i in range(start+1,stop):

images = np.concatenate((images, x_train[i].reshape([1,784])))

plt.imshow(images, cmap=plt.get_cmap(‘gray_r’))

plt.show()

现在开始构建和训练我们的模型的部分。首先我们定义一些变量来指定希望导入多少训练和测试样本。刚开始我会导入所有的数据，但是后面我会改变这个值来节省一些资源：

x_train, y_train = TRAIN_SIZE(55000)

Total Training Images in Dataset = (55000, 784)

————————————————–

x_train Examples Loaded = (55000, 784)

y_train Examples Loaded = (55000, 10)

那么这些代码到底是什么意思哪？在我们用的这个数据集里面，一共有55000个手写的从0到9的数字样本。每个样本都是一个28×28像素的图像，并被扁平化成一个包含784个值的数组，其中每个值代表了一个像素的灰度。之所以要被扁平化，是因为只有这样TensorFlow才能线性地使用它。上面的代码显示了在变量x_train 里面，我们导入了55000个样本，每个都包含784个像素。变量x_train 是一个55000行加784列的矩阵。变量y_train 包含了所有x_train 样本所对应的正确的标识。这里并没有用一个整数来存贮标识，而是用一个1×10的二元数组来存储。其中某一位数字为1就代表这个数字是它对应那个位置。这种方式也被叫做一热位编码（one-hot encoding）。下面的例子给出了代表数字7的数组。

图1 代表数字7的数组。来源：Justin Francis

让我们来随便找一张图片，并用我们上面定义的函数来读取扁平化的数据，重新排列它，再显示出来，并把它所对应的标识也打印出来（注意：想要继续编辑python代码，你需要关掉matplot打开的窗口）：

display_digit(ran.randint(0, x_train.shape[0]))

图2  [ 0.  0.  0.  0.  0.  0.  0.  1.  0.  0.] 来源：Justin Francis

下面是分类器使用的多个训练样本的扁平化的数据形式。当然，我们的分类器看到的是从零到一个代表灰度的数值，而不是看到的像素点。

display_mult_flat(0,400)

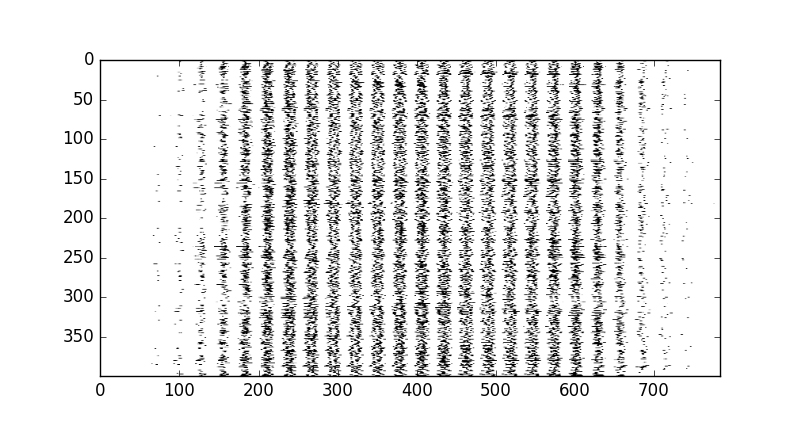
图3 前400个训练样本。来源：Justin Francis

到目前为止，我们还根本没用到TensorFlow。下一步就是导入TensorFlow，并定义我们的会话（session）。某种意义上说，TensorFlow会创建一个有向无环图，让你导入数据，并在一个会话里运行这个图。

import tensorflow as tf

sess = tf.Session()

接着我们定义一个占位符。顾名思义，占位符是一个用来导入数据的变量。唯一需要注意的就是，想要导入数据到这个变量，数据必须完全匹配占位符的尺寸（shape）和类型（type）。TensorFlow的官网是这样解释的：“一个占位符存在的意思仅仅是为了作为导入数据的目标。它并没有被初始化且不包含数据。”这里我们定义x占位符作为一个导入x_train数据的变量。

x = tf.placeholder(tf.float32, shape=[None, 784])

当我们把None分配给占位符时，就意味着这个占位符可以被导入任意数量的样本。在我们的例子里，这个占位符可以被导入任意多个有784列的值。

下面我们定义y_，用来导入y_train的数据。这个变量后面会被用来比较我们的分类预测与标准答案。这里可以认为我们的标识就是分类的类别。

y_ = tf.placeholder(tf.float32, shape=[None, 10])

接着我们定义权重 W和偏置量b。这两个变量是分类器里的普通工作者：它们是在训练完的分类器里，我们用来计算预测所需要的唯一的值。

首先我们把权重和偏置量都设为零，因为随后TensorFlow会自己优化这些值。注意：我们的权重W是一个784个值对应于10个分类的每一个类的集合。

W = tf.Variable(tf.zeros([784,10]))

b = tf.Variable(tf.zeros([10]))

我喜欢把这些权重看做是对应于10个数字的10张速查表。这和老师们用一个透明的速查表来给多选题目打分很类似。不幸的是对偏置量的解释有些超出这个教程的范畴，但我还是喜欢把它看成一个和权重相关的特殊关系。它们两个一起影响我们的最终答案。

现在我们来定义分类函数，即 y。这个特殊的分类器也被叫做多元逻辑回归。我们通过把每个扁平化的数字与我们的权重相乘，并加上偏置量来做出预测：

y = tf.nn.softmax(tf.matmul(x,W) + b)

让我们暂时先忽略softmax，直接看看softmax函数内部是什么样。matmul是矩阵相乘的函数。如果你了解矩阵相乘，你应该能较好地理解这个计算，并且知道x * W + b会产生一个训练样本数量(m)×分类的数量(n)的(m×n)的矩阵。

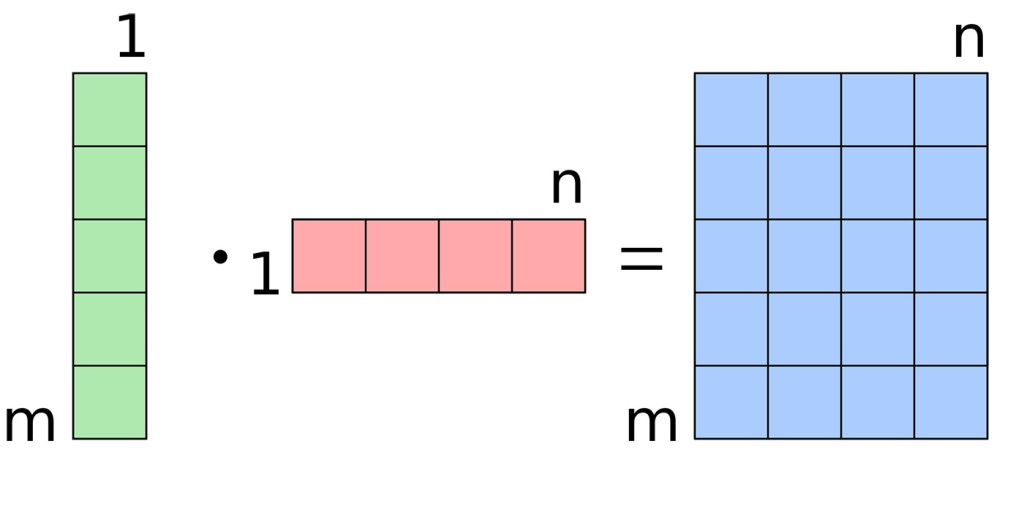
图4 简单的矩阵相乘。来源：Quartl on Wikimedia Commons

如果你还对此有疑惑，可以通过执行对y的输出来确认：

print(y)

Tensor(“Softmax:0”, shape=(?, 10), dtype=float32)

上面的输出结果告诉我们y在会话里什么，但如果我们是想看到y的实际值哪？由于不能通过直接打印一个TensorFlow图里面的对象来获得它的实际值，你必须运行一个给它导入数据的适当的会话。注意：如果你仅仅只是运行sess.run(y)，TensorFlow会提醒你需要给它导入数据。

x_train, y_train = TRAIN_SIZE(3)

sess.run(tf.global_variables_initializer())

#如果使用TensorFlow 0.12之前的版本，请用下面的命令:

#sess.run(tf.initialize_all_variables())

print(sess.run(y, feed_dict={x: x_train}))

[[ 0.1  0.1  0.1  0.1  0.1  0.1  0.1  0.1  0.1  0.1]

[ 0.1  0.1  0.1  0.1  0.1  0.1  0.1  0.1  0.1  0.1]

[ 0.1  0.1  0.1  0.1  0.1  0.1  0.1  0.1  0.1  0.1]]

现在我们可以看到对前三个训练样本的分类预测。到目前为止，我们的分类器什么也不知道。所以它就给出了一个平均的10%概率，来预测我们的三个样本在每个类别里的概率。

但是你可能会问TensorFlow是怎么知道这个概率的？它是通过计算softmax函数的结果来学习概率的。Softmax函数获得一系列数值，并设法让它们的和为1，并以此来获得每个值的概率。任何softmax值总是会被转换成大于0小于1。还是没搞清楚？可以试着运行下面的代码（译者注：在TensorFlow版本0.10运行会报错，版本0.11上正常），以了解softmax是怎么做数学计算的。

sess.run(tf.nn.softmax(tf.zeros([4])))

sess.run(tf.nn.softmax(tf.constant([0.1, 0.005, 2])))

接着定义我们的cross_entropy函数，也叫做损失或代价函数。它被用来衡量我们分类的结果的好坏。代价越高，则越不准确。它是通过比较预测的每个样本的y与y_train里面的真实值来计算准确度的。我们的目标是最小化这个损失。

cross_entropy = tf.reduce_mean(-tf.reduce_sum(y_ * tf.log(y), reduction_indices=[1]))

这个函数对所有的预测值y（值的范围是从0到1）进行log运算后和真实值y_进行矩阵元素相乘。如果值接近0，log计算后的值就是一个非常大的负值（例如，-np.log(0.01) = 4.6）；如果值接近1，log计算后的值就是一个小的负值（例如，-np.log(0.99) = 0.1）。

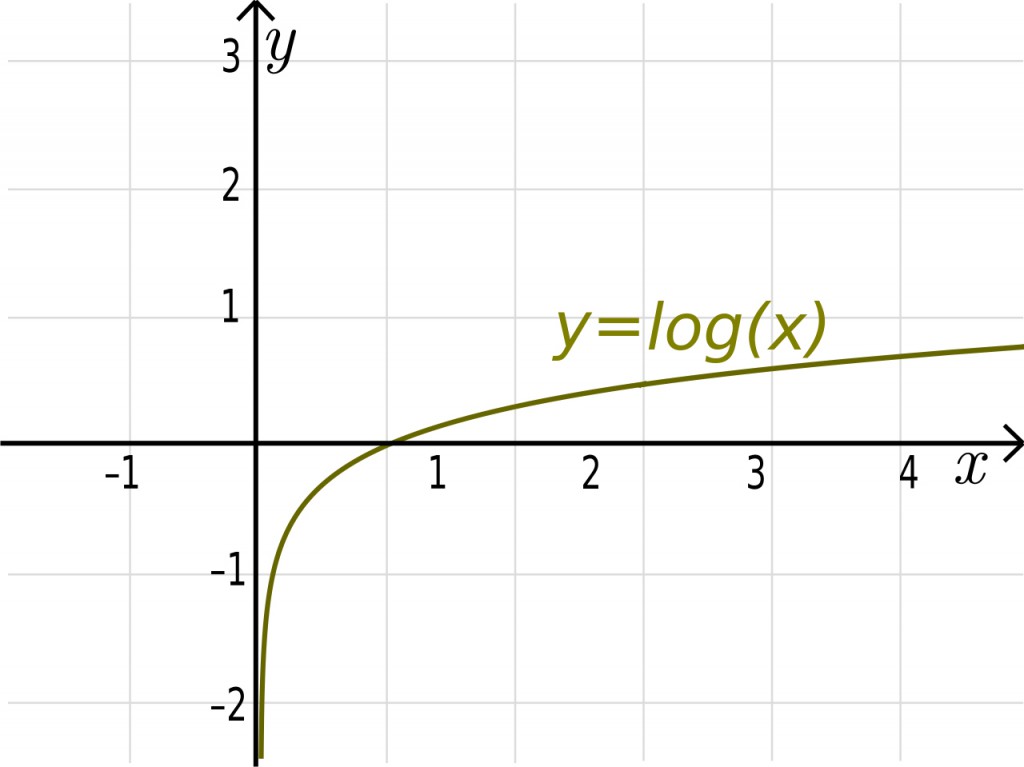
图5 Y = log (x)函数。来源Lfahlberg on Wikimedia Commons

本质上，如果预测结果是不对的但是置信度很高，我们就用一个很大的值来“惩罚”分类器；而如果结果是对的且置信度也很高，我们只用一个非常小的值。

下面是一个编造的python数组的例子。显示了softmax预测的结果是3且置信度很高。

j = [0.03, 0.03, 0.01, 0.9, 0.01, 0.01, 0.0025,0.0025, 0.0025, 0.0025]

让我用下面这个标识为3的数组作为基准来比较它和我们的softmax函数。

k = [0,0,0,1,0,0,0,0,0,0]

您能猜出损失函数会返回什么结果吗？你能看出下面对“j”进行log计算是如何对一个错误答案用一个非常大的负数进行惩罚的吗？运行下面的例子来试着理解吧。

-np.log(j)

-np.multiply(np.log(j),k)

上面会返回9个0和一个0.1053。加和后，我们就会认为这是一个不错的预测。下面看看如果我们的预测结果不变，但实际的正确答案是2的时候会怎么样。

k = [0,0,1,0,0,0,0,0,0,0]

np.sum(-np.multiply(np.log(j),k))

这次cross_entropy函数返回的是4.6051。意味着对我们错误的预测做了一个很严重的惩罚。之所以有这样的严重的惩罚，是因为分类器很有信心地认为是3，但真实值应该是2。

下面我们开始训练分类器。训练的目的就是找到合适的W和b值来得到尽可能小的损失值。

下面部分里，你可以自己修改一些变量的值。下面所有的全大写字母变量的值都是可以被修改和尝试的。实际上我很鼓励你这么做！先用例子里给出的这些值，然后你可以修改来得到更多或者更少的训练样本数量，或者是不同的学习率的值，再看看结果有什么不同。

如果你设定TRAIN_SIZE为一个很大的数，那么要有等一会的心理准备。任何时间，你都可以从这里开始再运行这些代码，并尝试不同的值。

x_train, y_train = TRAIN_SIZE(5500)

x_test, y_test = TEST_SIZE(10000)

LEARNING_RATE = 0.1

TRAIN_STEPS = 2500

现在我们可以初始化所有的变量了。初始化之后，TensorFlow的图才能够使用它们。

init = tf.global_variables_initializer()

#If using TensorFlow prior to 0.12 use:

#init = tf.initialize_all_variables()

sess.run(init)

我们需要使用梯度下降法来训练分类器。首先定义我们的训练方法以及一些测量准确度的变量。变量training将会基于选定的LEARNING_RATE（学习速率）执行梯度下降优化器，以期获得最小化的损失函数cross_entropy。

training = tf.train.GradientDescentOptimizer(LEARNING_RATE).minimize(cross_entropy)

correct_prediction = tf.equal(tf.argmax(y,1), tf.argmax(y_,1))

accuracy = tf.reduce_mean(tf.cast(correct_prediction, tf.float32))

我们定义一个循环，重复执行TRAIN_STEPS次。每循环一次，就运行一次training，使用feed_dict从x_train和y_train里输入训练样本。为了计算准确率，代码会运行来accuracy对x_test里没见过的数据进行分类并比较获得的y值和y_test的值。我们的测试数据必须是分类器没见过的，没有用于训练，这一点非常重要。如果一个老师给学生们一个小测验，而最后还用同样的试题来做期末考试，那么最终会得到一个对学生们掌握知识的程度的不准确的测量。

for i in range(TRAIN_STEPS+1):

sess.run(training, feed_dict={x: x_train, y_: y_train})

if i%100 == 0:

print(‘Training Step:’ + str(i) + ‘  Accuracy =  ‘ + str(sess.run(accuracy, feed_dict={x: x_test, y_: y_test})) + ‘  Loss = ‘ + str(sess.run(cross_entropy, {x: x_train, y_: y_train})))

为了对梯度下降的原理做可视化，你可以把损失想象为一个基于y_和y的784维的图像，其中包含不同的x、W和b值。如果你无法可视化784维，这很正常。我强烈建议你看看Chris Olah的这个博文来了解MNIST所涉及的维度问题。为了能更好更简单地解释这个问题，我们使用两维空间的函数y = x^2。

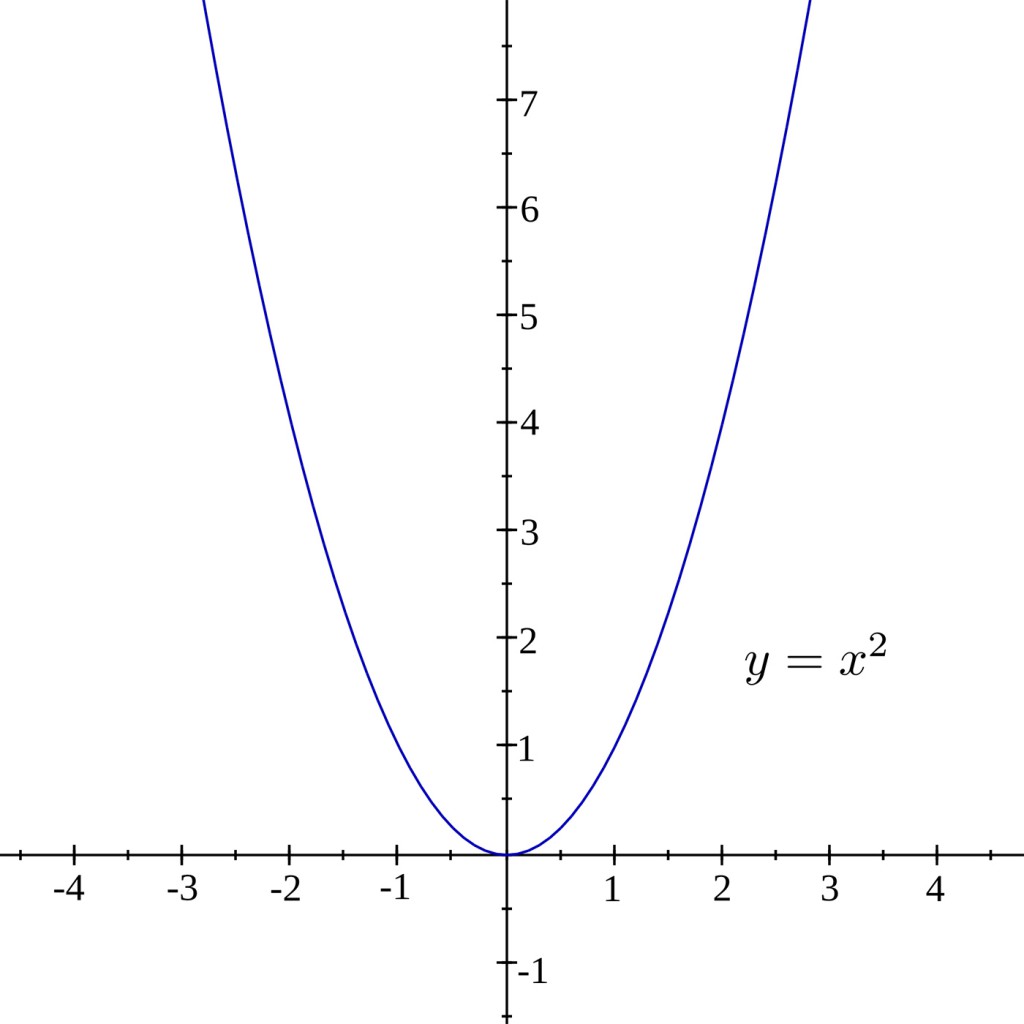
图6 抛物线y = x^2。来源: Adrignola on Wikimedia Commons

在循环的每一步中，依赖于cross_entropy的计算值的大小，分类器会根据LEARNING_RATE移动一步，向它认为会降低cross_entropy的方向前进一点。而这个更低的点则是由TensorFlow通过对cross_entropy求导数计算得出的。这个导数是在当前点的切线的斜率。在向这个新的点移动的时候，相应地W和b都会被改变，而斜率也在降低。在我们举的这个y = x^2例子里，这就意味着向X=0方向移动，也即最小化。如果这个学习速率非常小，那么分类器就会在训练过程中采用很小的步长；如果这个值太大，分类器的步长就会很大，那么就很可能“跨越”过真正的最小点。

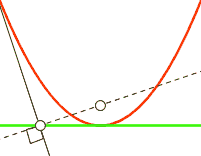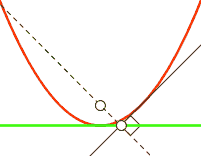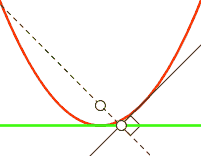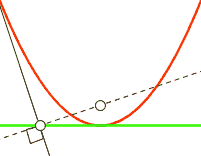
图7 实黑线显示的是在某个点的切线。来源：Tosha on Wikimedia Commons

有没有注意到上面例子里训练循环结束前的阶段，虽然损失还在降低但是准确率则是在略微地降低？这意味着我们还是可以持续地降低损失值，但是这对于预测未见过的测试数据并提高准确度并没有什么帮助。这也被称为过拟合（不能泛化）。使用代码给出的默认设置值，我得到了大概91%的准确率。如果我想通过作弊得到94%的准确率，我可以把测试样本数量取为100。这显示了如果没有充足的测试样本的话，你可能会得到一个有偏颇的准确率。

需要记住的是上面是计算我们的分类器的一个非常低效的方法。但我是故意这样做的，主要是为了学习和做实验。理想情况是当用一个非常大的数据集做训练时，可以采取小批次多次训练，而不是一次都训练完。如果你想学习这么做的话，可以看看TensorFlow网站上的这个教程。

下面到了我最喜欢的部分。我们已经计算出了权重的速查表，那么就用下面的代码把他们画出来吧。

for i in range(10):

plt.subplot(2, 5, i+1)

weight = sess.run(W)[:,i]

plt.title(i)

plt.imshow(weight.reshape([28,28]), cmap=plt.get_cmap(‘seismic’))

frame1 = plt.gca()

frame1.axes.get_xaxis().set_visible(False)

frame1.axes.get_yaxis().set_visible(False)

再可视化一下。

plt.show()

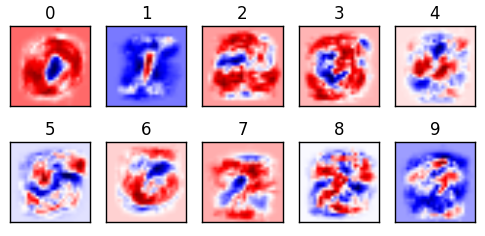
图8 来源：Justin Francis

上图对从0到9的权重值进行了可视化。这也是我们的分类器最重要的部分。这个机器学习的整个工作就是找出什么是最优的权重。一旦这些权重被计算出来，就可以用这个权重速查表来很容易地找到答案了。这也就是为什么神经网络可以很容易地被移植移动设备上。因为模型一旦训练好，就不再需要很多存储和计算资源来做计算了。我们的分类器就是通过比较测试样例和图里面的红色与蓝色区域去做预测的。认为越红的区域命中的概率越高；白色的区域是中性的，而蓝色的区域则是错误的。

所以现在让我们使用这个速查表来对一个样本进行分类。

x_train, y_train = TRAIN_SIZE(1)

display_digit(0)

看看得出的预测y。

answer = sess.run(y, feed_dict={x: x_train})

print(answer)

这是一个(1×10)的矩阵。每一列包含一个概率值。

[[  2.12480136e-05   1.16469264e-05   8.96317810e-02   1.92015115e-02

8.20863759e-04   1.25168199e-05   3.85381973e-05   8.53746116e-01

6.91888575e-03   2.95970142e-02]]

但这样的显示对我们不是很有用。因此我们用argmax函数来获得最高预测概率值的那个位置。

answer.argmax()

至此，让我们使用这个速查表来建立一个函数，对这个数据集里的一个随机选取的图片做识别。

def display_compare(num):

# THIS WILL LOAD ONE TRAINING EXAMPLE

x_train = mnist.train.images[num,:].reshape(1,784)

y_train = mnist.train.labels[num,:]

# THIS GETS OUR LABEL AS A INTEGER

label = y_train.argmax()

# THIS GETS OUR PREDICTION AS A INTEGER

prediction = sess.run(y, feed_dict={x: x_train}).argmax()

plt.title(‘Prediction: %d Label: %d’ % (prediction, label))

plt.imshow(x_train.reshape([28,28]), cmap=plt.get_cmap(‘gray_r’))

plt.show()

然后运行这个函数。

display_compare(ran.randint(0, 55000))

你能找到一个预测错误的例子吗？只要运行display_compare(2)，你就可以找到分类器做的一个错误的数字识别（把9认成4）。你觉得为什么对这个样本的分类会出错？

下面的部分是这个教程有趣的地方。看看下面的动画。注意当使用1到10个训练样本时对权重做的可视化了吗？很明显，训练数据很少的时候，模型很难有泛化的能力。下面的动画显示了权重是如何随着训练样本数量增加而变化的。你能发现是怎么变化的吗？

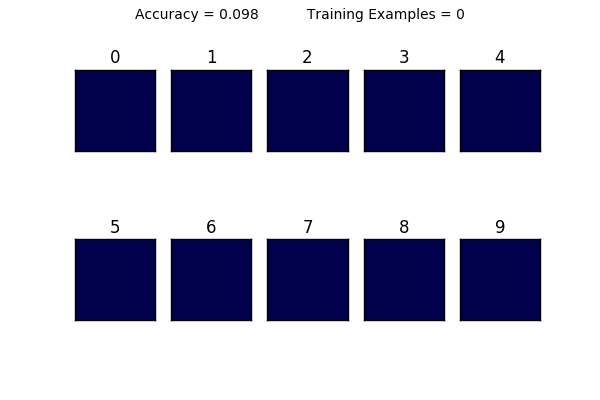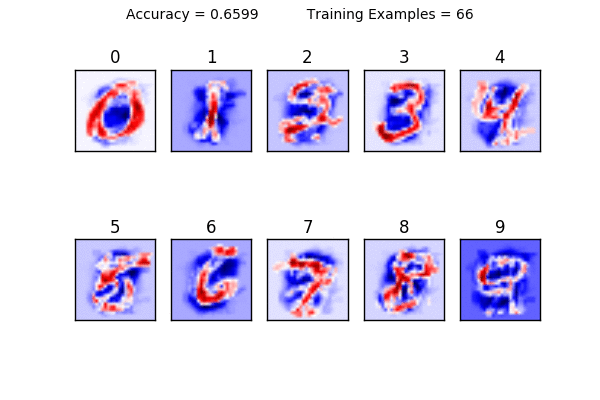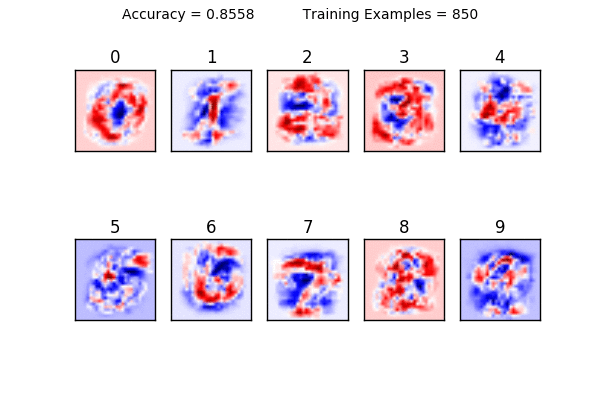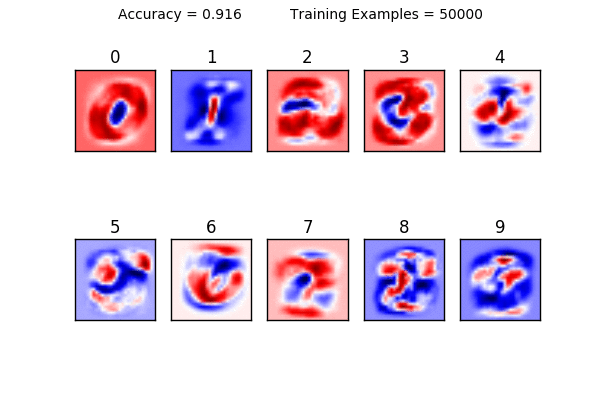
图9 来源：Justin Francis

你也可以看出一个线性分类器的局限性：在某个数量点后，用更多的数据训练并不能进一步提升准确率。如果我们试图去识别一个写在这个方形靠左边的数字“1”，你觉得会发生什么？分类器会很难做出识别，因为我们所有的训练样本的数字1都是在中间附近的。

希望这篇博文能帮助你更好地理解这个MNIST代码背后的故事。要注意的是，这个神经网络仅仅只有两层。这不是深度学习！想获得几近完美的准确率，我们必须开始卷积地深度思考。

如果你想更交互地运行这个会话，这里是我的GitHub库，其中包括一个Jupyter Notebook的版本。在写这个教程的过程中我很开心，也学到了很多。非常感谢你的阅读。真心希望你在看完这篇博文后，一些新的思路能在你的脑海中形成。