在一家人工智能优先的金融交易和咨询公司Hedged Capital我们使用概率模型在金融市场进行交易。 在这篇博客文章中，我们探讨了所有金融模型中固有的三类错误，并在TensorFlow Probability（TFP）中展示了一个简单的模型示例。

金融不是物理学

亚当·斯密，一般公认的现代经济学的创始人，对牛顿的力学和万有引力定律心存敬畏。 从那时候开始，经济学家们就一直致力于将他们的学科变成像物理学这样的科学。 他们渴望将能够在微观和宏观层面准确解释和预测人类经济活动的理论进行公式化。 这种欲望在20世纪初由欧文·费希尔（Irving Fisher）等经济学家一起凝聚成一种趋势，并在20世纪后期的经济物理学运动中达到顶峰。

图1. Mike Shwe和Deepak Kanungo的作图，经过许可使用

抛开现代金融学的所有复杂的数学不谈，它的理论是有严重缺陷的，与物理学相比的时候尤为如此。 例如，物理学可以用令人惊讶的精确度在计算机中预测月球的运动，以及电子的运动。 这些预测可以由任何物理学家在任何时间，地球上的任何地方计算出来。 相比之下，市场参与者在解释每日市场变动的原因，或在世界任何地方随时随地预测股票价格这一点上，会遇到大麻烦。

也许金融比物理更难。 与原子和钟摆不同，人是复杂的、具有自由意志和潜在认知偏见的感性生物。 他们倾向于具有不一致的表现，并且不断地对他人的行为做出反应。 此外，市场参与者通过击败人类运营的系统或者与其博弈来进行获利。

在投资南海公司后失去了一笔巨大财富后，牛顿曾经说过，“我可以计算出星体的运动，但却无法计算出人类的疯狂。”请注意，牛顿的资金可不是什么“傻钱”。他担任英国造币厂监督近31年，帮助英镑建立了持续两个多世纪的黄金成色标准。

所有的金融模型都是错的

模型用于简化现实世界的复杂性，从而使我们能够专注于我们感兴趣的现象中蕴含的特征。 显然，地图将无法捕捉其所建模的地形的丰富性。 着名的统计学家George Box曾有一句脍炙人口的打趣：“所有模型都是错的，不过有些很有用。”

这种观察特别适用于金融学。 一些学者甚至认为，金融模型不仅错误，而且危险; 物理科学的外表使经济模型的拥护者错误地觉得，这些模型预测能力的准确性是确定性的。 这种盲目的信仰给他们的信徒和整个社会带来了许多灾难性的后果。 文艺复兴科技（Renaissance Technologies）是历史上最成功的对冲基金，它对金融理论的批判性观点付诸实践。 他们宁愿雇用物理学家，数学家，统计学家和计算机科学家，也不聘请具有金融或华尔街背景的人。 他们使用基于非金融理论的量化模型来进行市场交易，这些理论包括信息论，数据科学和机器学习。

无论金融模型是基于学术理论还是基于历史数据的数据挖掘策略，它们都受到下面要详细介绍的三种建模错误的影响。 因此，所有模型都需要定量分析其预测中固有的不确定性。 分析和预测中的错误可能来自以下任何一类有问题的建模过程：使用不适当的函数形式，输入不准确的参数，或无法适应市场中的结构变化。

三种建模错误

1.模型定义中的错误：几乎所有的金融理论都在模型中使用正态分布。 例如，正态分布是Markowitz的现代投资组合理论和Black-Scholes-Merton期权定价理论的基础。 然而，有充分记录的事实表明，股票，债券，货币和商品都具有厚尾分布。 换句话说，极端事件的发生频率远高于正态分布索预测的频率。

如果资产的价格回报率是具有正态分布的，那么在任何时代都不会发生以下任何金融灾难：黑色星期一，墨西哥比索危机，亚洲货币危机，长期资本管理公司（Long Tem Capital Management）的破产（刚好，这家公司由两位诺贝尔经济学获奖者所领导），以及闪崩。 个别股票的“小型闪崩”的发生频率甚至高于这些宏观事件。

然而，由于其简单性和易于跟踪分析的特性，金融教科书、研究生金融项目和职业培训继续在其资产评估和风险模型中使用正态分布。 鉴于当今先进的算法和计算资源，这些原因已不再合理。 这种不情愿放弃正态分布的情况就是“酒鬼的搜索”的一个明显例证，这个原理来自于一个笑话，一个酒鬼在公园的黑暗中丢了钥匙，但他却在灯柱下疯狂搜索，因为这有灯光。

2.模型参数估计中的错误：这种类型的错误的出现，可能是因为市场参与者以不同的速度访问不同等级的信息。 他们对信息处理能力的复杂程度、认知偏差上也是不同的。 这些因素导致了对模型参数深刻的认知不确定性。

让我们考虑一下利率的特例。 作为任何金融资产估值的基础，利率用于对资产的不确定未来现金流进行折现，并估计其在当前的价值。 例如，在消费者层面，信用卡的可变利率与称为主利率的基准挂钩。 这一利率通常与联邦基金利率同步变化，联邦基金利率是对美国和世界经济具有重要意义的利率。

让我们假设你想从现在开始估算一年后信用卡的利率。 假设目前的主利率为2％，而您的信用卡公司则向您收取10％加上主利率。 鉴于当前经济的强势，您认为美联储更有可能提高利率。 美联储将在未来12个月内举行八次会议，并将联邦基金利率提高0.25％或将其保持在前值水平。

在下面的TFP代码示例中（参见完整代码：，我们使用二项分布来模拟您在12个月期间结束时的信用卡利率。 具体来说，我们将使用具有以下参数的TensorFlow概率二项分布类：total_count = 8（试验次数，即美联储会议次数），probs = {0.6,0.7,0.8,0.9}，是我们关于美联储在每次会议上将联邦基金利率提高0.25％这一事件概率的估计范围。

 ＃首先我们对假设进行编码

num_times_fed_meets_per_year = 8.

possible_fed_increases = tf.range(

start=0.,

limit=num_times_fed_meets_per_year + 1)

possible_cc_interest_rates = 2. + 10. + 0.25 * possible_fed_increases 

prob_fed_raises_rates = tf.constant([0.6, 0.7, 0.8, 0.9]) 

 ＃现在我们使用TFP以矢量化方式进行概率计算

 ＃填充维度，使得美联储加息概率和信用卡利率进行广播计算

 prob_fed_raises_rates = prob_fed_raises_rates […，tf.newaxis]

 prob_cc_interest_rate = tfd.Binomial （

 TOTAL_COUNT = num_times_fed_meets_per_year，

 probs = prob_fed_raises_rates）.prob（possible_fed_increases） 

在下图中，注意到，12个月内信用卡利率的概率分布如何主要取决于您对八次会议中每次会议加息的可能性的估计。 您可以看到，随着对每次美联储会议加息概率的估计每增加0.1，您的信用卡在12个月内的预期利率将增加约0.2％。

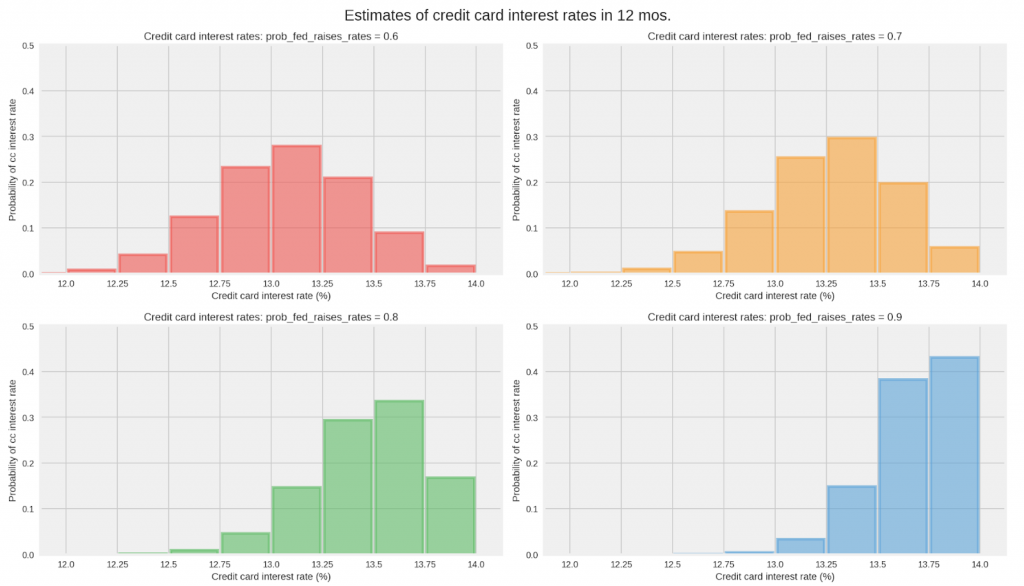
图2. Josh Dillion和Deepak Kanungo作图。 经许可使用

即使所有市场参与者在他们的模型中使用二项分布，也很容易看出他们如何对未来的主利率存在分歧，因为他们对概率的估计存在差异。 实际上，这个参数很难估计 。 许多机构都有专职的分析师，包括美联储的前员工，用分析美联储的每一份文件、演讲和事件的方法，试图估计这个参数。

回想一下，我们假设这个概率参数probs在我们的模型中对于接下来的八次美联储会议中的每一次都是不变的。 这有多现实？ 利率设定机构联邦公开市场委员会（FOMC）的成员可不仅仅是一组有偏的硬币。 他们可以并且确实做到了根据经济如何随时间变化来改变他们的个人偏见。 假设参数probs在未来12个月内保持不变，不仅不现实，而且风险也很大。

3.因为无法适应市场结构变化导致的错误：潜在生成基础数据的随机过程可能随时间变化，换句话说，随机过程不是稳定遍历的。 我们生活在充满活力的资本主义经济中，其特点是技术创新和不断变化的货币和财政政策。 资产价值和风险的分布随着时间变化，这是规律，而不是例外。 对于此类分布，基于历史数据定下的参数值必然会将错误引入预测。

在上面的例子中，如果经济显示出放缓的迹象，美联储可能会决定在第四次会议中采取更中立的立场，让你将probs参数从70％改为50％。 您的probs参数的这一变化将反过来改变您的信用卡利率预测。

有时，时变分布及其参数会连续变化或跳变，如墨西哥比索危机。 对于连续变化或跳变，所使用的模型需要适应不断变化的市场条件。 很可能我们需要一个具有不同参数的新函数形式来解释和预测新制度中的资产价值和风险。

假设在我们的例子第五次会议之后，美国经济遭受外部极端冲击 – 比如说希腊新的民粹主义政府决定拖欠债务。 现在美联储可能更有可能降息而不是提高利率。 鉴于美联储前景的这种结构性变化，我们将不得不将模型中的二项概率分布改为具有适当参数的三项分布。

结论

金融不是像物理学那样精确的预测科学，相去甚远。 因此，我们不要将学术理论和金融模型像量子物理模型那样进行处理

所有金融模型，无论是基于学术理论还是数据挖掘策略，都受三种建模错误的影响。 虽然可以使用适当的建模工具弱化这三个错误，但却无法消除。 信息和认知偏见总是存在不对称性。 由于资本主义，人类行为和技术创新的动态性质，资产价值和风险模型将随着时间的推移而变化。

金融模型需要一个框架来量化时变随机过程预测中固有的不确定性。 同样重要的是，框架需要根据基于实质性新数据集，不断更新模型和/或模型参数。 这些模型必须使用小数据集进行训练，因为基础环境可能变化太快而导致无法收集大量相关数据。

致谢

我们感谢TensorFlow Probability团队，特别是Mike Shwe和Josh Dillon，感谢他们在此博客文章的早期草稿中提供的帮助。

参考

1.金钱公式，作者David Orrell和Paul Wilmott，Wiley出版社，2017年

2.胡扯诺贝尔奖，作者：J.R. Thompson，L.S. Baggett，W.C. Wojciechowski和E.E. Williams，后凯恩斯主义经济学杂志，2006年秋季

3.模型错误，由作者：Katerina Simons，新英格兰经济评论，1997年11月

4.贝叶斯风险管理，作者：Matt Sekerke，Wiley出版社，2015年