如果使用TensorFlow的所有较高级别的工具，例如tf.contrib.learn和Keras，你可以轻松地使用非常少量的代码来构建卷积神经网络。但是经常使用这些较高级别的应用，你就没法看到它们内部的代码，从而缺失了对这些应用背后所发生的事情的理解。

在本教程中，我会介绍如何只使用低级别的TensorFlow工具从零开始构建卷积神经网络，以及使用TensorBoard可视化我们的计算图和网络的表现。如果你还不了解全连接神经网络的一些基础知识，我强烈建议你首先查看这篇《这不是另外一个使用TensorFlow来做MNIST数字图像识别的教程》。在本文中我也会把卷积神经网络的每个步骤分解到绝对基础的程度，以便你可以完全了解计算图中的每个步骤。通过从零开始构建该模型，你可以轻松地将计算图的各方面可视化，以便可以看到每层卷积并使用它们做出你自己的推断。我会只强调主要代码，如果想查看全部代码，你可以在GitHub上找到相应的Jupyter Notebook文件。

获得一个数据集

一开始我需要决定要使用哪个图像数据集。我决定用牛津大学视觉几何团队的宠物数据集。我之所以选择这个数据集，是因为它很简单且有很好的标注，同时训练数据也足够多，而且还有对象边界区域标注——如果我以后想训练一个对象检测模型就可以使用该信息。另一个我认为对于构造第一个模型非常好的数据集是在Kaggle上发现的辛普森数据集，其中有很多可用于训练的简单数据。

选择模型

接下来，我必须决定使用哪个卷积神经网络的模型。非常流行的一些模型包括GoogLeNet或VGG16，它们都具有多个卷积层可用于检测具有1000多个类别的ImageNet数据集。不过我要使用一个更简单的四层卷积网络：

图1 图片由Justin Francis友情提供

我们分解一下这个模型。它从一张224x224x3的图像开始，在三个通道上通过卷积得到32个特征图。我们将这组32个特征图一起卷积得到另外32个特征。 然后将其池化得到112x112x32的图像，随后两次卷积得到64个特征，最后池化到56x56x64。然后将这个最终池化的层的每个单元全连接到512个神经元上，并基于类别的数量最后连接到softmax层。

处理和构建数据集

首先我们开始加载依赖项，其中包括一组我所编写的imFunctions函数，它可以帮助来处理图像数据。

import imFunctions as imf

import tensorflow as tf

import scipy.ndimage

from scipy.misc import imsave

import matplotlib.pyplot as plt

import numpy as np

然后，我们可以使用imFunctions下载和提取图像。

imf.downloadImages(‘annotations.tar.gz’, 19173078)

imf.downloadImages(‘images.tar.gz’, 791918971)

imf.maybeExtract(‘annotations.tar.gz’)

imf.maybeExtract(‘images.tar.gz’)

我们可以将图像分到不同的文件夹，包括训练和测试文件夹。 sortImages函数中的参数数值表示测试数据跟训练数据的百分比。

imf.sortImages(0.15)

接着使用一个相应的one hot向量将我们的数据集构建成一个numpy数组以表示我们的类别。它还也会从所有的训练和测试图像中减去图像的平均值，这是在构建卷积网络时的标准化动作。该函数会询问你要包括哪些类别——由于我有限的GPU 内存（3GB），我选择了一个非常小的数据集，试图区分两种狗：柴犬和萨摩耶犬。

train_x, train_y, test_x, test_y, classes, classLabels = imf.buildDataset()

卷积和池化是如何工作的

现在我们有了一个可用的数据集，不过让我们先停一下，看看卷积的最底层是如何工作的。在跳到彩色卷积滤波器之前，让我们来看一张灰度图以确保能弄明白每个细节。让我们编写一个7×7的滤波器可用于四个不同的特征图。TensorFlow的conv2d函数相当简单，它有四个变量：输入、滤波器、步幅、填充方式。在TensorFlow网站上是这么描述conv2d函数的：

对于给定的4维输入和滤波器张量计算一个2维卷积。

输入是一个维度为[batch，in_height，in_width，in_channels]的一个张量，滤波器/核张量的维度是[filter_height，filter_width，in_channels，out_channels]。

因为我们正在处理灰度图像，所以in_channels是1，而我们应用了四个滤波器，所以out_channels将会是4。我们将图2里所示的四个滤波器/核应用到一张图像或每批批次一张。

图2 图像由Justin Francis友情提供

让我们来看下这个过滤器是如何影响我们输入的灰度图像的。

gray = np.mean(image,-1)

X = tf.placeholder(tf.float32, shape=(None, 224, 224, 1))

conv = tf.nn.conv2d(X, filters, [1,1,1,1], padding=”SAME”)

test = tf.Session()

test.run(tf.global_variables_initializer())

filteredImage = test.run(conv, feed_dict={X: gray.reshape(1,224,224,1)})

tf.reset_default_graph()

这会返回一个4维(1, 224, 224, 4)的张量，我们可以用来可视化这四个滤波器：

图3 图像由Justin Francis友情提供

很明显可以看到滤波器内核的卷积是非常强大的。将其分解，我们的7×7内核每次以1的步幅覆盖49个图像像素，将每个像素的值乘以每个内核值，然后将所有49个值加在一起以构成一个像素。如果你对图像滤波器内核的思想仍然觉得没有感觉，我强烈推荐这个网站——他们在内核可视化方面做得非常出色。

实质上，大多数卷积神经网络都包含卷积和池化。最常见的是，一个用于卷积的3×3内核滤波器。特别是，以2×2的步幅和2×2内核的最大值池化是基于内核中的最大像素值来缩小图像的一种激进方式。下图展示的是一个内核为2X2和两维上步幅都为2的简单例子。

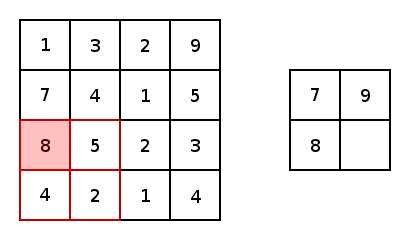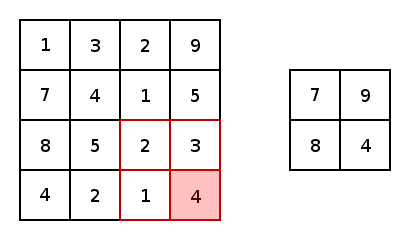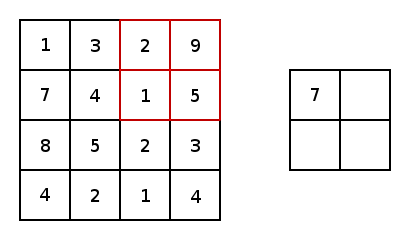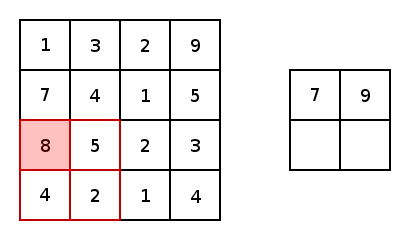
图4 图片由Justin Francis友情提供

对于conv2d和最大值池化，它们都有两个填充选项：“VALID”会缩小输入图像；“SAME”会通过在输入图像边缘周围添加零来保持输入图像大小。下图是一个内核为3×3步幅为1×1的最值大池化的示例，展示了不同的填充选项的结果：

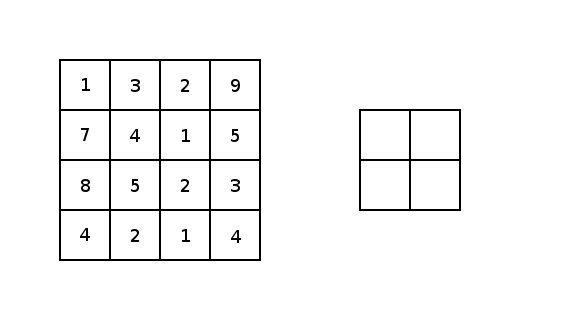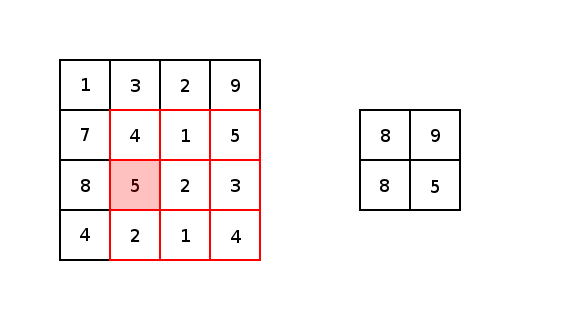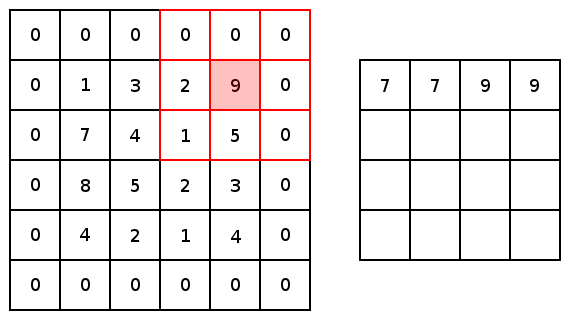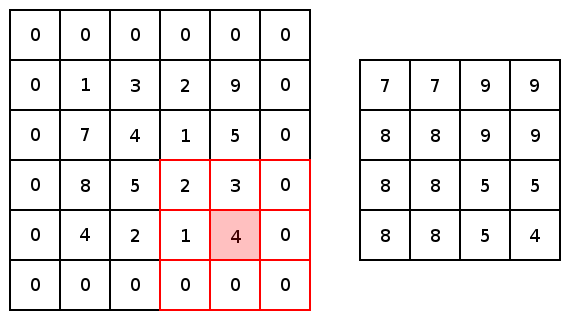
图5 图像由Justin Francis友情提供

构建卷积神经网

我们已经介绍了基本知识，现在让我们开始构建我们的卷积神经网络模型。我们可以从占位符开始。 X是我们的输入符，我们将把图像输入到X中，Y_是一组图像的真实类别。

X = tf.placeholder(tf.float32, shape=(None, 224, 224, 3))

Y_ = tf.placeholder(tf.float32, [None, classes])

keepRate1 = tf.placeholder(tf.float32)

keepRate2 = tf.placeholder(tf.float32)

我们将在一个命名空间内创建每个过程的所有部分。命名空间对以后在TensorBoard中可视化计算图是非常有用的，因为它们将所有东西都打包成一个可扩展的对象。我们创建了第一组内核大小为3×3的滤波器，需要三个通道分别输出32个滤波器。这意味着32个滤波器中的每一个R、G和B通道都会有3×3的内核权重。非常重要的是我们滤波器的权重值是使用截断正太分布来初始化的，所以会有多个随机滤波器使TensorFlow能适用于我们的模型。

# CONVOLUTION 1 – 1

with tf.name_scope(‘conv1_1′):

filter1_1 = tf.Variable(tf.truncated_normal([3, 3, 3, 32], dtype=tf.float32, stddev=1e-1), name=’weights1_1′)

stride = [1,1,1,1]

conv = tf.nn.conv2d(X, filter1_1, stride, padding=’SAME’)

biases = tf.Variable(tf.constant(0.0, shape=[32], dtype=tf.float32), trainable=True, name=’biases1_1′)

out = tf.nn.bias_add(conv, biases)

conv1_1 = tf.nn.relu(out)

在第一层卷积的最后，conv1_1使用了relu函数，它是将每个负数赋值为零的阈。然后我们将这32个特征跟另外的32个特征做卷积。你可以看到conv2d的输入是第一个卷积层的输出。

# CONVOLUTION 1 – 2

with tf.name_scope(‘conv1_2′):

filter1_2 = tf.Variable(tf.truncated_normal([3, 3, 32, 32], dtype=tf.float32,

stddev=1e-1), name=’weights1_2′)

conv = tf.nn.conv2d(conv1_1, filter1_2, [1,1,1,1], padding=’SAME’)

biases = tf.Variable(tf.constant(0.0, shape=[32], dtype=tf.float32),

trainable=True, name=’biases1_2′)

out = tf.nn.bias_add(conv, biases)

conv1_2 = tf.nn.relu(out)

然后进行池化将图像缩小一半。

# POOL 1

with tf.name_scope(‘pool1′):

pool1_1 = tf.nn.max_pool(conv1_2,

ksize=[1, 2, 2, 1],

strides=[1, 2, 2, 1],

padding=’SAME’,

name=’pool1_1′)

pool1_1_drop = tf.nn.dropout(pool1_1, keepRate1)

最后一部分涉及到在池化层上使用dropout（我们将在后面更详细地介绍）。然后紧接着是使用64个特征的两个卷积和另一个池化。请注意第一个卷积必须将先前的32个特征通道转换为64。

# CONVOLUTION 2 – 1

with tf.name_scope(‘conv2_1′):

filter2_1 = tf.Variable(tf.truncated_normal([3, 3, 32, 64], dtype=tf.float32,

stddev=1e-1), name=’weights2_1′)

conv = tf.nn.conv2d(pool1_1_drop, filter2_1, [1, 1, 1, 1], padding=’SAME’)

biases = tf.Variable(tf.constant(0.0, shape=[64], dtype=tf.float32),

trainable=True, name=’biases2_1′)

out = tf.nn.bias_add(conv, biases)

conv2_1 = tf.nn.relu(out)

 

# CONVOLUTION 2 – 2

with tf.name_scope(‘conv2_2′):

filter2_2 = tf.Variable(tf.truncated_normal([3, 3, 64, 64], dtype=tf.float32,

stddev=1e-1), name=’weights2_2′)

conv = tf.nn.conv2d(conv2_1, filter2_2, [1, 1, 1, 1], padding=’SAME’)

biases = tf.Variable(tf.constant(0.0, shape=[64], dtype=tf.float32),

trainable=True, name=’biases2_2′)

out = tf.nn.bias_add(conv, biases)

conv2_2 = tf.nn.relu(out)

 

# POOL 2

with tf.name_scope(‘pool2′):

pool2_1 = tf.nn.max_pool(conv2_2,

ksize=[1, 2, 2, 1],

strides=[1, 2, 2, 1],

padding=’SAME’,

name=’pool2_1′)

pool2_1_drop = tf.nn.dropout(pool2_1, keepRate1)

接下来我们创建一个含有512个神经元全连接的网络层，它将与我们的大小为56x56x64的pool2_1层的每个像素建立一个权重连接。这会有超过1亿个不同的权重值！为了计算全连接的网络，我们必须将输入展开到一维，然后就可以乘以权重并加上偏置项。

#FULLY CONNECTED 1

with tf.name_scope(‘fc1′) as scope:

shape = int(np.prod(pool2_1_drop.get_shape()[1:]))

fc1w = tf.Variable(tf.truncated_normal([shape, 512], dtype=tf.float32,

stddev=1e-1), name=’weights3_1′)

fc1b = tf.Variable(tf.constant(1.0, shape=[512], dtype=tf.float32),

trainable=True, name=’biases3_1’)

pool2_flat = tf.reshape(pool2_1_drop, [-1, shape])

out = tf.nn.bias_add(tf.matmul(pool2_flat, fc1w), fc1b)

fc1 = tf.nn.relu(out)

fc1_drop = tf.nn.dropout(fc1, keepRate2)

然后是softmax及其相关的权重和偏置，最后是我们的输出Y.

#FULLY CONNECTED 3 & SOFTMAX OUTPUT

with tf.name_scope(‘softmax’) as scope:

fc2w = tf.Variable(tf.truncated_normal([512, classes], dtype=tf.float32,

stddev=1e-1), name=’weights3_2′)

fc2b = tf.Variable(tf.constant(1.0, shape=[classes], dtype=tf.float32),

trainable=True, name=’biases3_2′)

Ylogits = tf.nn.bias_add(tf.matmul(fc1_drop, fc2w), fc2b)

Y = tf.nn.softmax(Ylogits)

创建损失函数和优化器

现在可以开始训练我们的模型。首先必须决定批量大小，我不能使用批量大小超过10以防止耗尽GPU内存。然后必须确定周期的数量，它是指算法循环遍历所有分批的训练数据的次数，最后是我们的学习速率α。

numEpochs = 400

batchSize = 10

alpha = 1e-5

然后我们为交叉熵、精度检查器和反向传播优化器指定范围。

with tf.name_scope(‘cross_entropy’):

cross_entropy = tf.nn.softmax_cross_entropy_with_logits(logits=Ylogits, labels=Y_)

loss = tf.reduce_mean(cross_entropy)

with tf.name_scope(‘accuracy’):

correct_prediction = tf.equal(tf.argmax(Y, 1), tf.argmax(Y_, 1))

accuracy = tf.reduce_mean(tf.cast(correct_prediction, tf.float32))

with tf.name_scope(‘train’):

train_step = tf.train.AdamOptimizer(learning_rate=alpha).minimize(loss)

接着就可以创建我们的会话和初始化我们所有的变量。

sess = tf.Session()

init = tf.global_variables_initializer()

sess.run(init)

创建TensorBoard用的汇总

现在我们要使用TensorBoard，以便可以看到分类器工作的表现怎么样。我们将创建两个图：一个用于我们的训练集，一个用于我们的测试集。我们可以通过使用add_graph函数来可视化我们的计算图。我们将使用汇总标量来衡量我们的总体损失和准确性，并将我们的汇总合并到一起以便只需调用write_op来记录标量。

writer_1 = tf.summary.FileWriter(“/tmp/cnn/train”)

writer_2 = tf.summary.FileWriter(“/tmp/cnn/test”)

writer_1.add_graph(sess.graph)

tf.summary.scalar(‘Loss’, loss)

tf.summary.scalar(‘Accuracy’, accuracy)

tf.summary.histogram(“weights1_1”, filter1_1)

write_op = tf.summary.merge_all()

训练模型

现在我们可以开始编写进行评估和训练的代码。我们不希望每步的损失和准确性都使用汇总记录器来记录，因为这会大大减慢分类器的训练速度。因此我们会每五步记录一次。

steps = int(train_x.shape[0]/batchSize)

for i in range(numEpochs):

accHist = []

accHist2 = []

train_x, train_y = imf.shuffle(train_x, train_y)

for ii in range(steps):

#Calculate our current step

step = i * steps + ii

#Feed forward batch of train images into graph and log accuracy

acc = sess.run([accuracy], feed_dict={X: train_x[(ii*batchSize):((ii+1)*batchSize),:,:,:], Y_: train_y[(ii*batchSize):((ii+1)*batchSize)], keepRate1: 1, keepRate2: 1})

accHist.append(acc)

 

if step % 5 == 0:

# Get Train Summary for one batch and add summary to TensorBoard

summary = sess.run(write_op, feed_dict={X: train_x[(ii*batchSize):((ii+1)*batchSize),:,:,:], Y_: train_y[(ii*batchSize):((ii+1)*batchSize)], keepRate1: 1, keepRate2: 1})

writer_1.add_summary(summary, step)

writer_1.flush()

 

# Get Test Summary on random 10 test images and add summary to TensorBoard

test_x, test_y = imf.shuffle(test_x, test_y)

summary = sess.run(write_op, feed_dict={X: test_x[0:10,:,:,:], Y_: test_y[0:10], keepRate1: 1, keepRate2: 1})

writer_2.add_summary(summary, step)

writer_2.flush()

#Back propigate using adam optimizer to update weights and biases.

sess.run(train_step, feed_dict={X: train_x[(ii*batchSize):((ii+1)*batchSize),:,:,:], Y_: train_y[(ii*batchSize):((ii+1)*batchSize)], keepRate1: 0.2, keepRate2: 0.5})

 

print(‘Epoch number {} Training Accuracy: {}’.format(i+1, np.mean(accHist)))

 

#Feed forward all test images into graph and log accuracy

for iii in range(int(test_x.shape[0]/batchSize)):

acc = sess.run(accuracy, feed_dict={X: test_x[(iii*batchSize):((iii+1)*batchSize),:,:,:], Y_: test_y[(iii*batchSize):((iii+1)*batchSize)], keepRate1: 1, keepRate2: 1})

accHist2.append(acc)

print(“Test Set Accuracy: {}”.format(np.mean(accHist2)))

可视化计算图

在训练过程中，让我们通过在终端中激活TensorBoard来检查运行情况。

tensorboard –logdir=”/tmp/cnn/”

可以将Web浏览器指向默认的TensorBoard地址http://0.0.0.0/6006。让我们先来看看我们的计算图模型。

正如你所看到的，通过使用命名空间属性我们可以直观地看到计算图模型的一个相当简洁的版本。

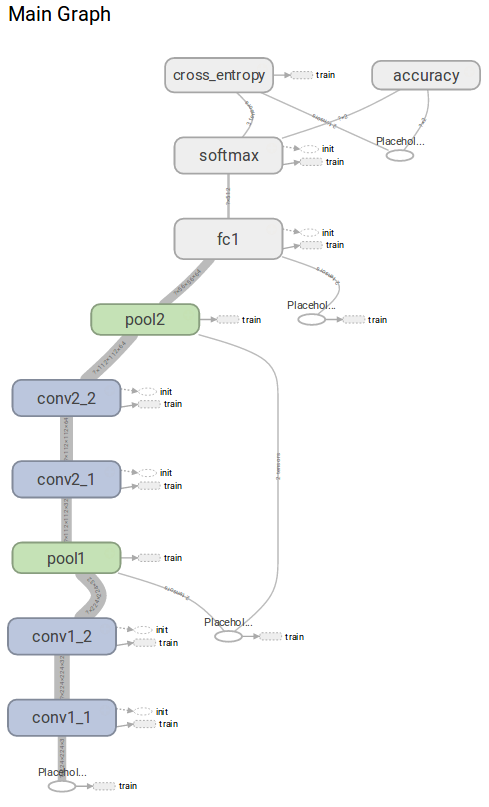
图6 图片由Justin Francis友情提供

性能表现评估

让我们看看准确性和损失标量随时间变化的情况。

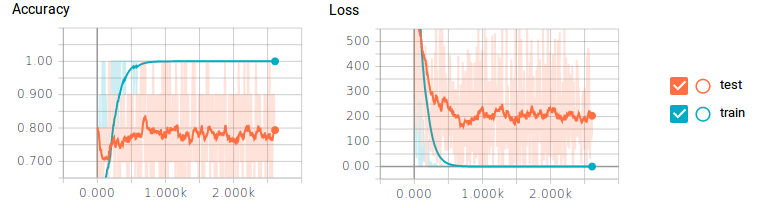
图7 图片由Justin Francis友情提供

你可能会看到这里出了一个很大的问题。对于训练数据，分类器达到了100％的准确度和0%的误差损失，但是测试数据的准确度最多只能达到80％而且还有很大的损失。这就是一个明显的过拟合——一些典型的原因包括没有足够的训练数据或神经元数量太多。

我们可以通过调整图片大小、对它们进行缩放和旋转来创建更多的训练数据，但更简单的方法是将dropout添加到池化层和全连接层的输出中。这会在每次训练中随机切割或丢弃一个图层中的部分神经元。这将迫使我们的分类器一次只训练一部分神经元，而不是所有神经元。这允许神经元专注于特定的任务，而不是所有神经元一起关注。丢弃80％的卷积层和50％全连接层的神经元会产生惊人的效果。

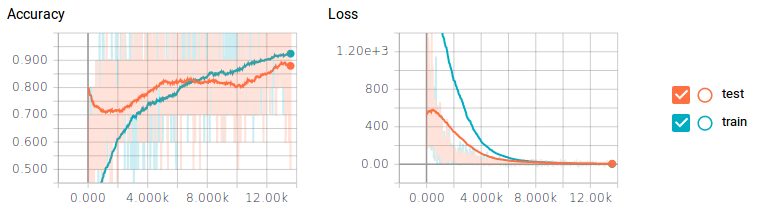
图8 图片由Justin Francis友情提供

仅仅通过丢弃神经元，测试数据的准确度就几乎能达到90％——性能几乎提高了10％！但代价是分类器花了大约6倍的时间才完成训练。

可视化不断进化的滤波器

为了增加乐趣，我让一个过滤器每训练50个步就产生一张图片，并制作了一个随滤波器权重进化的gif图像。这带来了非常酷的效果，并能很好地帮助理解卷积网络的是如何工作的。以下是来自conv1_2的两个滤波器：

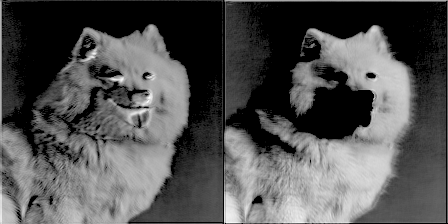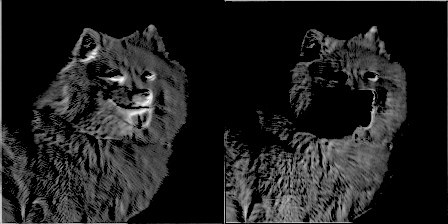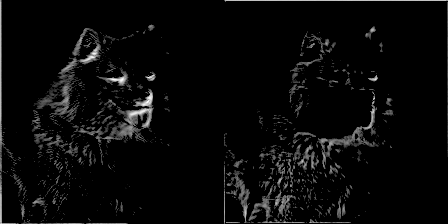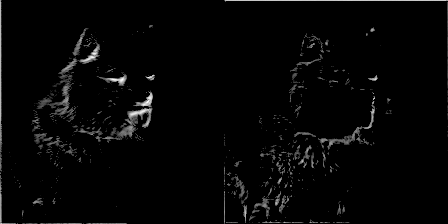
图9 图片由Justin Francis友情提供

你可以看到最初的权重初始化显示了图像的大部分，但随着时间推移权重不断更新，它们变得更加专注于检测某些边缘。令我惊讶的是，我发现第一个卷积核心filter1_1几乎没有改变。似乎初始权重本身已经足够好了。继续深入到网络层conv2_2，你可以看到它开始检测更抽象的广义特征。

图10 图片由Justin Francis友情提供

总而言之，使用了不到400个训练图像训练了一个几乎可以达到90％准确率的模型，这给我留下了深刻的印象。我相信如果有更多的训练数据和进行更多的超参数调整，我可以取得更好的结果。

行文到此，我们介绍了如何使用TensorFlow从零开始创建卷积神经网络、如何从TensorBoard中得出推论以及如何可视化滤波器。重要的是记住使用少量数据来训练分类器时，更容易的方法是选取一个已经使用多个GPU在大型数据集上训练好的模型和权重（如GoogLeNet或VGG16），并截断最后一层用自己的类别替换它们。然后所有分类器要做的就是学习最后一层的权重，并使用已存在的训练好的滤波器权重。所以，我希望你从这篇文章中获得一些东西，然后继续探索，从中得到乐趣，不断实验学习，再秀一些酷的东西！

这篇博文是O’Reilly和TensorFlow的合作产物。请阅读我们的编辑独立声明。